7443. Декомпозиция графа
Однажды Жомарт
решал задачу маршрутизации на сетях. Он обнаружил, что его граф ориентированный
и ациклический. Когда Серик пришел посмотреть на задачу, он был удивлен тем,
что имеется множество способов декомпозиции графа Жомарта в набор реберно
непересекающихся путей. Друзья уже начали думать, сколькими способами это можно
сделать. Пожалуйста, помогите им.
Вход. Первая строка содержит два целых числа n и m
(1 ≤ n ≤ 1000, 1 ≤ m ≤ 499500). Каждая из следующих m строк содержит два целых числа i, j
означающих что в графе имеется ориентированное ребро из вершины i в вершину j.
Выход. Выведите одно
число – ответ к задаче по модулю 109 + 7.
Пример. Имеются две возможные
декомпозиции:
1) два пути: 1 → 2 → 3
и 1 → 3;
2) три пути: 1 → 2, 2 →
3 и 1 → 3
|
Пример
входа |
Пример
выхода |
|
3 3 1 2 2 3 1 3 |
2 |
РЕШЕНИЕ
комбинаторика
Анализ алгоритма
Рассмотрим
сколькими способами можно провести декомпозицию ребер в каждой вершине.
Произведение этого числа способов для каждой вершины и есть ответ.

Пусть вершина
имеет x входящих и y исходящих ребер. Поскольку граф
следует разбить в набор реберно непересекающихся путей, то можно выбрать i ребер из x входящих, которые будут продолжать i путей, то есть пройдут через вершину и уйдут из нее через i исходящих ребер. Остальные входящие
ребра будут заканчивать свои пути в вершине, остальные исходящие – начинать
пути в вершине.

Количество
способов выбрать i ребер из входящих
и i ребер из выходящих равно ![]() . Однако эти i
ребер еще можно переставить между собой, то есть указанное количество способов
следует умножить на i!
. Однако эти i
ребер еще можно переставить между собой, то есть указанное количество способов
следует умножить на i!
Таким образом
количество способов провести декомпозицию одной вершины равно
f(x, y)
= ![]()
Пусть in[i] содержит количество входящих ребер в
вершину i, out[i] содержит количество ребер, исходящих из вершины i (1 ≤ i ≤ n). Тогда
ответом к задаче будет
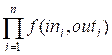
Напомним, что
все вычисления следует производить по модулю 109 + 7.
Пример
Ориентированный
граф из примера имеет два варианта декомпозиции:
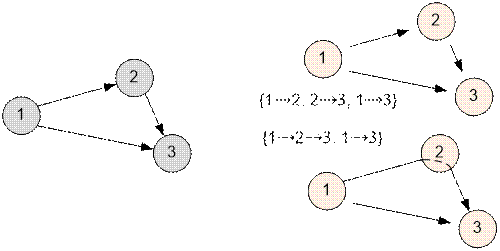
Рассмотрим варианты декомпозиции вершины с двумя
входными и двумя выходными ребрами.
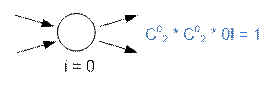
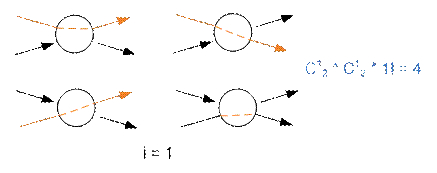
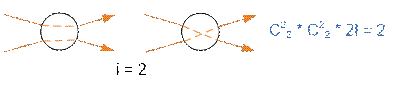
Таким образом f(2, 2) = 1 + 4 + 2 = 7.
Рассмотрим количество вариантов декомпозиции графа:

Ответ равен
 = f(0, 1) * f(1, 1) * f(1, 1) *
f(1, 0) = 4
= f(0, 1) * f(1, 1) * f(1, 1) *
f(1, 0) = 4
Возможными
декомпозициями будут:
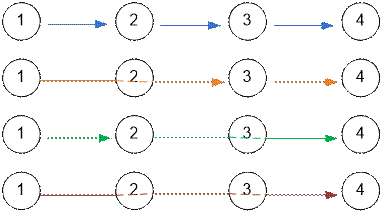
Рассмотрим
следующий пример.
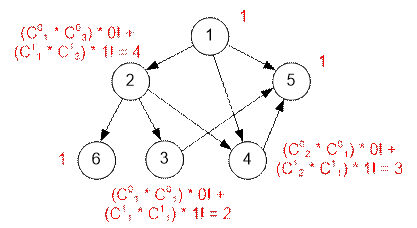
Количество
декомпозиций графа равно 4 * 2 * 3 = 24.
Реализация алгоритма
Объявим рабочие массивы.
#define MOD 1000000007LL
#define MAX 1110
long long
c[MAX][MAX], in[MAX], out[MAX], fac[MAX];
Пусть вершина имеет x
входящих и y исходящих ребер. Тогда
количество способов провести ее декомпозицию равно f(x, y).
long long
f(int x, int y)
{
long long ans = 0;
for(int i = 0; i <= min(x,y); i++)
ans = (ans + (((c[x][i] * c[y][i]) % MOD) *
fac[i]) % MOD) % MOD;
return ans;
}
Основная часть программы. Обнуляем массивы.
scanf("%d %d",&n,&m);
memset(c,0,sizeof(c));
memset(in,0,sizeof(in));
memset(out,0,sizeof(out));
memset(fac,0,sizeof(fac));
Заполняем массив биномиальных коэффициентов: c[i][j]
= ![]() .
.
c[0][0] = 1;
for(i = 0; i < MAX; i++)
c[i][0] = 1;
for(i = 1; i < MAX; i++)
for(j = 1; j
<= i; j++)
c[i][j] = (c[i-1][j] + c[i-1][j-1]) % MOD;
Заполняем массив факториалов.
fac[0] = 1;
for(i = 1; i < MAX; i++)
fac[i] = (fac[i-1] * i) % MOD;
Читаем ребра ориентированного графа. Заполняем массивы
входящих in и выходящих out ребер.
for(i = 0; i < m; i++)
{
scanf("%d
%d",&x,&y);
out[x]++;
in[y]++;
}
Вычисляем произведение способов, которыми можно провести
декомпозицию ребер в каждой вершине.
ans = 1;
for(i = 1; i <= n; i++)
ans = (ans * f(in[i], out[i])) % MOD;
Выводим ответ.
printf("%lld\n",ans);